統計検定1級の難易度は?統計数理・統計応用の違いからおすすめ勉強法まで解説
「統計検定1級ってどんな資格?」
「統計検定1級の難易度が知りたい!」
統計検定1級の受験を考えている方は、このように思っているのではないでしょうか。
この記事では、統計検定1級の難易度、統計数理・統計応用の出題範囲、おすすめの参考書や勉強法など、統計検定1級に合格するための情報をご紹介しています。
統計検定1級は難しすぎて受験しようか迷っているという方も、統計検定1級の受験をためらうことはありません。
勉強法の詳細や頻出範囲の解説もありますので、ぜひ参考にして合格を目指しましょう!
統計検定1級についてざっくり説明すると
- 統計検定1級は統計数理と統計応用の2つの試験に合格する必要がある
- 統計検定1級は大学の専門課程を修了しているレベルであり、合格にはかなりの勉強時間が必要
- 難易度がかなり高い試験であるため、数学や統計学を学んだことがない方の勉強法としては、講座の受講がおすすめ
統計検定1級の試験の概要
統計検定1級は、毎年11月に開催されています。準1級の試験内容を前提とし、社会で必要とされるあらゆる分野でのデータ解析の能力があるかを問う試験です。
試験の内容は大学の専門課程(3年生、4年生)を修了しているレベルであり、かなり難易度が高いと言えます。
統計検定1級では、統計解析法や数理的な知識について正しく理解していることが求められます。
試験は統計数理と統計応用で分割
統計検定1級は、下位の級とは異なり2つの試験があり、午前は「統計数理」、午後は「統計応用」という構成になっています。
統計数理は、統計学を数理的な側面から見た試験です、確率や確率分布などが出題されます。
統計応用は、統計学を実践的に活用するために特に知っておくべき内容を理解しているかが問われる試験です。
この二つの試験に合格することで統計検定1級の資格が取得できます。
試験は会場受験だけ
統計検定1級は会場での筆記試験のみです。
2級、3級はコンピュータで受験するCBT方式ですので好きなタイミングで受験できます。しかし、1級は決められた日時に会場まで行って受験しなければなりません。この点は多少不便であると言えます。
また、2級、3級、4級は年に2回受験できますが、1級の試験は年に1回しか受験できません。2級以下と比べると取得できる機会が限られており、不合格の場合1年後にしか再チャレンジできませんので、入念な受験対策をしておく必要があります。
試験科目と範囲
試験は統計数理、統計応用ともに論述式で行われます。試験時間はそれぞれ90分です。
統計数理では5問出題されその中の3問を試験時に選択します。
統計応用は、まず「人文科学」「社会科学」「理工学」「医薬生物学」の4つの分野から一つを試験の申込時に選択します。
統計応用では、その選択した分野の試験のみの受験で大丈夫です。出題数は、5問出題され試験時に3問を選択します。
出題範囲は以下のとおりです。
統計数理の出題範囲
| 大項目 | 小項目 | 具体的項目 |
|---|---|---|
| 確率と確率変数 | 事象と確率 | 確率の計算、条件付き確率、ベイズの定理など |
| 確率分布と母関数 | 確率関数、累積分布関数、条件付き分布など | |
| 確率母関数、モーメント母関数(積率母関数) | ||
| 分布の特性値 | モーメント、四分位数、偏相関係数など | |
| 変動変換 | 変動変換、確率変数の線形結合 | |
| 極限定理と確率分布の近似 | 大数の弱法則、中心極限定理 | |
| 二項分布の正規近似とポアソン近似、少数法則、連続修正 | ||
| 種々の確率分布 | 離散型分布 | 一様分布、超幾何分布、多項分布など |
| 連続型分布 | 一様分布、ガンマ分布、多変量正規分布など | |
| 標本分布 | t分布、カイ二乗分布、F分布 | |
| 統計的推測(推定) | 母集団と標本・統計量 | 十分統計量、ネイマンの分解定理、順序統計量 |
| 尤度と最尤推定 | 尤度関数、有効スコア関数、最尤推定など | |
| 各種推定法 | モーメント法、最小二乗法、線形推定(BLUE)など | |
| 点推定量の性質 | 不偏性、十分性、推定量の相対効率など | |
| モデル評価基準 | カルバック・ライブラー情報量、情報量規準AIC、クロスバリデーション | |
| 漸近的性質など | クラーメル・ラオの不等式、フィッシャー情報量(1次元)、デルタ法など | |
| 区間推定 | 信頼係数、信頼区間の構成、被覆確率 | |
| 統計的推測(検定) | 検定の基礎 | 仮説、有意水準、検出力(検定力)など |
| 検定法の導出 | ネイマン・ピアソンの基本定理、ワルド型検定、スコア型検定など | |
| 正規分布に関する検定 | 平均値と分散に関する検定、複数の平均に関する検定 | |
| 種々の検定法 | 二項分布、適合度の検定、ノンパラメトリック検定など | |
| 解析法の考え方と各種分析手法 | 分散分析 | 一元配置分散分析、交互作用、多重比較など |
| 回帰分析 | 線形単回帰、重相関係数平均への回帰(回帰効果)など | |
| 分割表の解析 | カイ二乗検定、マクネマー検定、イェーツの補正など | |
| ノンパラメトリック法 | 符号検定、ウィルコクソン符号付き順位和検定、順位相関係数など | |
| 不感染データ | 欠測(欠損)、打ち切り、トランケーション | |
| シミュレーション | 乱数、MCMC、ブートストラップなど | |
| ベイズ法 | 事前分布、階層ベイズモデル、ギブスサンプリングなど |
統計応用の出題範囲
| 大項目 | 小項目 | 具体的項目 |
|---|---|---|
| 共通した事項 | 確率・統計の基礎事項(統計検定2級の範囲)に加え、各応用分野に共通した事項 | |
| 研究の種類 | 実験研究、観察研究、調査 | |
| 標本調査法 | 完全無作為抽出、二段階抽出、サンプルサイズの設計など | |
| 実験計画法 | フィッシャーの3原則、ブロック化、一部実施要因計画など | |
| 重回帰分析 | 重回帰モデル、一般化最小二乗推定、多重共線性など | |
| 多種多変量解析法 | 主成分分析、ロジスティック回帰分析、サポートベクターマシンなど | |
| 確率過程 | マルコフ連鎖、ポアソン過程、ブラウン運動など | |
| 時系列解析 | ARIMAモデル、状態空間モデル | |
| 人文科学分野 | 想定分野:文学、心理、教育、社会、地理、言語、体育、人間科学 | |
| データの取得法 | 実験と準実験、アンケート調査の設計と実践 | |
| データの集計 | クロス集計、連関の指標、四分相関など | |
| 多変量データ分析法 | 数量化理論、多次元尺度構成法、(確証的、探索的)因子分析など | |
| 潜在構造モデル | 潜在特性、潜在クラス分析 | |
| テストの分析 | テストの信頼性・妥当性、困難度、クロンバックのアルファなど | |
| 社会科学分野 | 想定分野:経済、経営、社会、政治、金融工学、保険 | |
| 調査の企画と実施 | 標本誤差、無作為抽出、集落抽出など | |
| 重回帰モデルとその周辺 | 重回帰分析、多重共線性、変数選択 | |
| 計量モデル分析 | 外生変数、連立方程式モデル、切断回帰モデルなど | |
| 時系列解析 | トレンド、自己回帰、指数平滑化法 | |
| パネル分析 | 固定効果モデル、変量効果モデル、ハウスマン検定 | |
| 経済指数 | 経済指数(総合指数、景気判断指数)、ジニ係数、ローレンツ曲線など | |
| 理工学分野 | 想定分野:数学、物理、化学、地学、工学、環境 | |
| 多変量解析法 | 多変量正規分布、分散共分散行列、固有値・固有ベクトルなど | |
| 確率過程 | ランダムウォーク、マルコフ連鎖、ARIMA過程など | |
| 線形推測 | 線形モデル、線形結合の分布、線形制約 | |
| 漸近理論 | 大数の法則、漸近分散、デルタ法など | |
| 品質管理 | 管理図、保全性、工程能力指数など | |
| 実験計画 | 実験の計画と実施、変量効果、交略法など | |
| 医薬生物学分野 | 想定分野:医学、私学、薬学、疫学、公衆衛生、看護学、生物学、農・林・水産学 | |
| 研究の種類 | 介入研究と観察研究、コホート研究、臨床試験など | |
| データ収集法 | 無作為抽出と無作為割り付け、盲検化、プラセボ対照など | |
| 処置効果 | 効果の大きさ、サロゲートエンドポイント、サンプルサイズ設計 | |
| 効果の指標 | 変化量、相対リスク、ハザードなど | |
| カテゴリカルデータ解析 | カイ二乗検定、分割表の解析、対数線形モデル | |
| ノンパラメトリック法 | ウィルコクソン順位和検定(マン・ホイットニーU検定)、順位相関係数、マクネマー検定など | |
| 交略の調整 | 交略、標準化、SMRなど | |
| 生存時間と繰り返し測定 | 生存時間解析、カプラン・マイヤー法、比例ハザードなど | |
| 検査の性能評価 | 検査の感度・特異度、ROC曲線 |
このように、統計検定1級は非常に幅広い出題範囲になっています。準1級までは浅く広い知識で対応できましたが、1級では頻出分野を中心にしっかり理解していることが必要であるため、勉強時間を多めに確保して学んでいきましょう。
統計検定1級の試験難易度を徹底考察
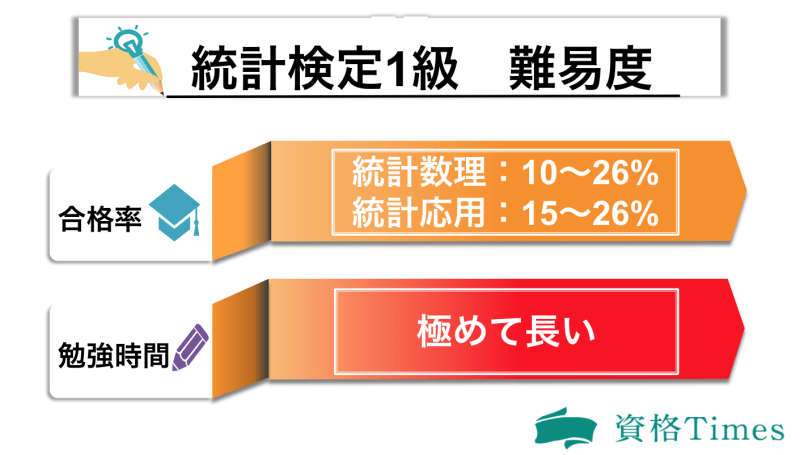
統計検定1級は、統計検定の中でも最高峰の難易度です。その理由としては、
- 他の級と異なり、理論分野と応用分野に分かれており、それぞれで合格が必要であること
- 合格率20%前半の試験が2つあり、負担が重いこと
- 全て論述式であり、深い理解が問われる試験内容であること
という3点があります。
各試験の合格率を紹介
以下では統計数理と統計応用の2015年~2019年までの合格率を紹介していきます。また、配点や合格点について注意すべき点もご紹介します。
各試験の合格率の推移は以下のとおりです。
統計数理
統計数理は、2015年は10.7%だったものの、その後は20%台に落ち着いています。合格率20%台という数字自体は、資格試験全体でみると非常に低い部類に入るため、統計数理は難関試験であると言えるでしょう。
統計応用
統計応用は、人文科学、社会科学、理工学、医薬生物学から得意分野を一つ選べるとはいえ、統計数理同様難易度が高い試験です。
特に2018年、2019年は10%台にまで合格率が下がっており、難易度がさらに高くなっています。
配点と合格点
1級では配点や合格点について公表されていません。そのため、絶対合格できるという目安はなく、どのくらいの勉強時間を設定すればよいかもわからないため、受験勉強は困難を極めます。
また、統計検定1級を取得するには、統計数理での合格と、統計応用での1分野以上での合格両方が必要になるのも取得のハードルが高い要素の一つです。
ただ、統計数理、統計応用の片方だけ合格した場合には、試験合格の有効期間が10年あります。
有効期間10年以内にもう片方にも合格すれば試験に合格でき、1級を取得することができます。
統計検定1級合格のための勉強法は2種類
統計検定1級は、統計学の知識や考え方に精通していないと一人で内容を理解していくことは難しいでしょう。
勉強法には独学か講座の受講の2種類がありますが、統計検定1級の場合、専門的な知識があることが前提であるため、独学の難易度はかなり高いと言えます。
以下では、独学と講座の受講それぞれの勉強法に向いている人の特徴をご紹介します。
独学での学習に必要な条件
独学の場合、次の条件のどれかは必ず満たしていないと、合格することは難しいでしょう。
統計学の基本がしっかり身についている人
統計検定1級を受験するにあたって、統計学の基本が身に付いていることは必須です。具体的には、準1級レベルまでの内容については精通していなければなりません。また、数学への深い理解も必要です。
1級の試験内容は大学で学ぶような専門的な内容であるため、統計学の基礎がわからないまま対策をしようとしても、内容が全く理解できないという事態に繋がってしまいます。
1級を受けるためには、まずは統計学の基本が身に付いてることが前提となります。
難関試験に独学で合格した経験を持っている人
統計検定1級の独学は、一般的な資格・検定と比較してもかなり難しい部類に入ると言えます。
そのため、以前例えば、難関大学や難関資格のような、難易度の高い試験に独学で合格したことがある人は有利になるでしょう。
数学や統計学を深く学ぶ学部に属している人
もともと大学で数学や統計学を学ぶ学部に在籍しており、難易度の高い数学や統計学の基礎を学んでいた人は、基礎的な知識があるため独学に向いている人の条件に当てはまります。
講座を使った勉強がおすすめの方
ここまでご紹介した独学に向いている人の条件にあてはまらなかった人は、講座で勉強することがおすすめです。
ここからは、講座での勉強が向いている人の具体例をご紹介していきます。
統計や数学の前提知識に自信のない人
統計学や数学の知識がない人、多少知識があっても準1級レベルまでに達していない人は、まず数理統計の基本を学べる講座を受講した方がよいでしょう。
1級は基礎的な知識がないまま合格できるほど甘くありません。わかりやすい講座を利用して、1級の受験に必須となる知識を確実に習得しましょう。
スケジュール管理が苦手な方
勉強の継続に自信のない方、勉強のスケジュール管理が苦手な方も講座が向いています。やるべき量と内容が決まっているため、講座を受講することで、勉強を継続的に続けられる確率が上がります。
受講の日程が決められている講座もあるので、それを上手く利用すれば途中で投げ出すことなく勉強を続けることができるでしょう。
本格的に学習を進めたい人におすすめの講座
1級の内容を本格的に学びたい人は、「すうがくぶんか」の統計検定1級対策講座の受講検討がおすすめです。
この講座では、統計学講座への長年の取り組みを生かして、独自のカリキュラムを考案して生徒のハイレベル知識養成を徹底サポートしています。
特に、記述式は対人指導でじっくり指導してくれることから、試験で通用する実力を確実に身につけられるでしょう。
独学で統計検定1級を勉強する場合
先ほども述べたように、独学で統計検定1級の勉強をすることは非常に難易度が高いと言えます。
それでも、もし独学で勉強すると決めたなら、あらかじめ必要な情報を徹底的に集めておくことが必要です。
まずは頻出範囲を押さえよう
統計数理では、多様な確率分布を問う問題は頻出範囲となります。
統計応用でも確率分布は頻出範囲であることから、確率分布については確実に得点できる対策が必須です。
また、推定量に関する問題も多く出題されますので、こちらも対策が必要になります。
応用分野はどれを選択するべきか
統計応用では「人文科学」「社会学」「理工学」「医薬生物学」の4つの分野があり、選択に迷うところです。
選択の基準としては、数理系の統計が得意な場合は、確率分布など統計数理に関わる問題が多く出題される「理工学」を選ぶのがおすすめです。
それ以外の場合は、自分が大学時代に学んでおり、ある程度理解度が高い分野を選ぶのがよいでしょう。
頻出分野ごとの対策法
統計検定1級に合格するには、頻出分野で点数を取ることが重要です。ここからは、統計検定1級で頻出する分野ごとの具体的な勉強法について解説します。
確率分布
確率分布の対策法としては、まず頻出範囲の分布について覚えておく必要があります。具体的には、確率密度関数やモーメント母関数などです。
また、スムーズに分布を使いこなす上では、確率分布同士の関係性を捉えることも必須となります。例えば、一様分布を指数分布に変える変数変換などが挙げられます。
検定・推定問題
検定・推定の方法は無数にあります。頻出のものを中心に、使い方と実際の使用例を押さえていくことが大切です。
具体的には、
- 不偏推定量
- 一致推定量
- 正規分布や二項分布の条件設定からの検定・推定
などが挙げられます。
線形代数の基礎も学習しておくとなおよい
統計学や機械学習を学ぶ際には、線形代数の知識が求められる場面が多くなります。
具体的には
- 計画行列の立式
- 正規方程式の取り扱い
- 多変量確率分布の変数変換におけるヤコビアンの計算方法
などが挙げられます。
特に、一定の線形モデルを仮定し計画行列を立て、推定量分散について評価するタイプの問題は、1級では頻出の問題です。そのため、線形代数の知識を身に付けておけば、これらのテーマに対応しやすくなります。
過去問は必ず解く
ここまでご紹介した頻出分野の内容理解を深めただけでは、実際に問題を解いたときに速く解くことはできません。
問題を何度も解いて慣れていくことにより、インプットした知識を素早くアウトプットできるようになります。
特に過去問を解くときには、ただ問題をひたすら解くのではなく、必ず時間制限を設けて解いていくことが必要です。
一問あたりに使う時間については、実際の試験時間90分から、一問にどれくらい時間をかけられるか考えて設定をしましょう。
解き終わった後の復習が大切
解き終わったあと、間違えた部分はそのままにせず参考書を見直して復習することが大切です。
間違えた部分をしっかり復習することで、苦手な部分を把握できるようになります。苦手な部分を復習して理解度が高まれば、次回から問題を解くスピードが速くなったり得点が上がったりしますので、自身の成長を実感することができるでしょう。
おすすめの参考書
ここからは、統計検定1級合格のためにおすすめできる参考書をご紹介していきます。
数理統計分野の勉強におすすめ
『数理統計学』は、確率数学や情報数学の基本概念をもとに、統計数理をわかりやすく解説した一冊です。
近代数学を学んでいる学生向けの参考書であるため、数学の知識は必要ですが、数学の知識がある方には読みやすい内容になっています。実際の口コミでの評価も高いためおすすめです。
線形代数も同時に学びたい人向けの1冊
『チャート式シリーズ 大学教養 線形代数』は、高校数学チャート式シリーズの例題方式などの特徴をそのまま備えており、大学数学の線形代数をわかりやすく学ぶことができます。
例題が多く内容も充実しているため、数学の知識があまりない初学者の方でも線形代数を理解しやすい一冊です。
統計応用向けの参考書
『基礎系 数学 確率・統計II (東京大学工学教程)』は、統計応用で頻出する実験計画法の背景まで学べる良書だと言えます。
本書のページ数は150ページで、内容を凝縮して解説されているため取り組みやすいところもポイントです。土台から知識を固めたい人におすすめできます。
過去問演習は公式問題集がおすすめ
『日本統計学会公式認定 統計検定 1級・準1級 公式問題集[2018〜2019年]』は、日本統計学会が唯一公式認定している問題集です。
1級、準1級の過去問が掲載されているため、1級の理解度を測れるのはもちろん、準1級までの知識の復習もできます。
統計検定1級についてまとめ
統計検定1級についてまとめ
- 統計数理、統計応用の片方だけ合格した場合には、試験の有効期間10年以内にもう片方にも合格すれば試験に合格できる
- 統計応用で選ぶ分野として、数理系の統計が得意なら統計数理の問題が多く出題される理工学を選ぶのがおすすめ
- 確率分布、検定・推定問題、線形代数は頻出なのでそれぞれしっかり対策をしよう
統計検定1級は合格率が20%であることや、統計数理、統計応用それぞれに合格しなければならないこと、論述式であることという3点から、非常に難易度が高い試験であると言えます。
しかし、大学で統計学や数学を学んだ方であれば独学でも合格を目指せます。ただし、演習量を多くする必要がありますので、知識があっても勉強時間は長く取りましょう。
また、統計学や数学の知識に自信がない方は、講座を受講してまずは基礎的な知識を学ぶところから勉強を始め、徐々に専門的な内容を学んでいくのがおすすめです。
統計検定1級の合格は簡単ではありませんが、頻出分野を把握し演習を積んで知識を定着させることで、合格を目指していきましょう。



![日本統計学会公式認定 統計検定 1級・準1級 公式問題集[2018〜2019年]](https://ws-fe.amazon-adsystem.com/widgets/q?_encoding=UTF8&MarketPlace=JP&ASIN=4788925516&ServiceVersion=20070822&ID=AsinImage&WS=1&Format=_SL250_&tag=shikakutimes-22)









